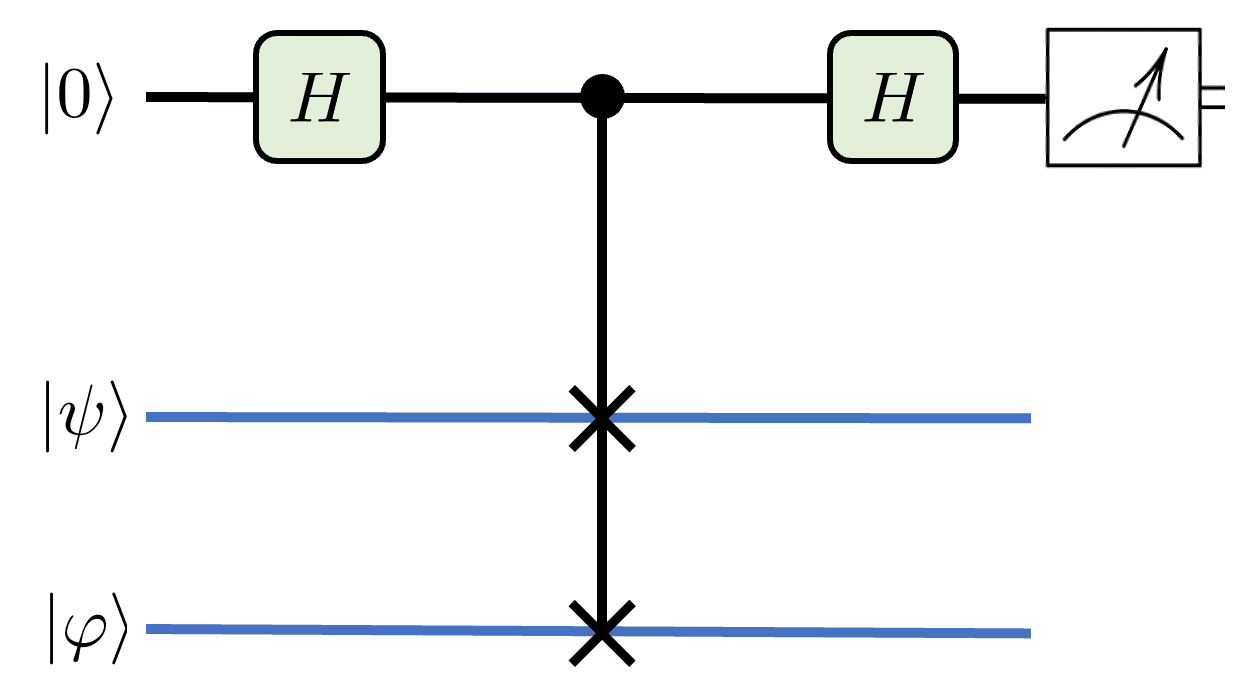
Le Test de Hadamard représente une avancée majeure dans le domaine de l’informatique quantique. En facilitant le passage entre différents états quantiques, cet outil joue un rôle clé dans la compréhension et l’exploitation des propriétés uniques des qubits. Cet article explore les fondements du Test de Hadamard, son fonctionnement et son importance dans les algorithmes quantiques modernes.
Origine et Principes du Test de Hadamard
Le Test de Hadamard repose sur la transformée de Hadamard, une opération mathématique essentielle qui permet de générer des superpositions d’états quantiques. En appliquant cette transformation, un qubit initialement dans un état donné est placé dans une superposition, offrant ainsi de multiples possibilités de calcul simultanées. Cette capacité à créer des superpositions est au cœur des bénéfices que l’informatique quantique peut offrir.
Fonctionnement du Test de Hadamard
Pour exécuter le Test de Hadamard, un qubit est soumis à la matrice de Hadamard, notée H. L’application de cette matrice envoie l’état de base |0⟩ ou |1⟩ du qubit dans un état de superposition, exprimé comme (|0⟩ + |1⟩)/√2. Cette superposition permet aux ordinateurs quantiques de réaliser des calculs qui seraient inaccessibles pour les machines classiques, car elles peuvent évaluer plusieurs chemins computationnels en même temps.
Applications Pratiques du Test de Hadamard
Le Test de Hadamard est utilisé dans divers algorithmes quantiques, notamment dans l’algorithme de Shor, qui mène à la factorisation rapide de grands nombres. De plus, cet outil est également essentiel dans l’optimisation des circuits quantiques, permettant une réduction significative de la complexité des calculs. Grâce à son efficacité, le Test de Hadamard constitue donc un atout incontournable dans l’arsenal des techniques d’informatique quantique.
Importance dans l’Éducation en Informatique Quantique
Comprendre le Test de Hadamard est primordial pour quiconque souhaite se plonger dans le monde de l’informatique quantique. Cet outil ne se limite pas à un usage mathématique ; il représente un pont vers des concepts plus avancés tels que l’enchevêtrement et les circuit quantiques. Par conséquent, sa maîtrise est essentielle pour développer des compétences solides dans ce domaine en pleine expansion.
Le Test de Hadamard se révèle être un outil fondamental en informatique quantique, permettant de manipuler et d’explorer les états de superposition des qubits. Adroitement utilisé, il transforme les états de base en superpositions, ce qui ouvre la voie à une multitude d’applications dans le cadre des algorithmes quantiques. Cette opération non seulement amplifie les capacités de calcul, mais souligne également l’importance de l’enchevêtrement et de la mesure quantique. En facilitant une meilleure compréhension des systèmes quantiques, le Test de Hadamard constitue un pilier dans le développement de solutions quantiques innovantes.
Le Test de Hadamard est une méthode essentielle en informatique quantique, permettant non seulement d’explorer les propriétés des qubits, mais aussi de démontrer des concepts fondamentaux tels que l’enchevêtrement et la superposition. Dans cet article, nous allons examiner les principes de base de ce test, son importance dans les algorithmes quantiques, ainsi que ses applications pratiques.
Compréhension des Qubits et de la Superposition
Avant de plonger dans le Test de Hadamard, il est crucial de comprendre ce qu’est un qubit. Contrairement à un bit classique, qui ne peut être que dans l’état 0 ou 1, un qubit peut être dans une superposition de ces deux états. Cela signifie qu’il peut représenter simultanément 0 et 1, ce qui élargit considérablement les capacités de calcul. La superposition est le fondement de nombreux algorithmes quantiques, permettant une exécution parallélisée des calculs.
Le Rôle de la Matrice de Hadamard
La matrice de Hadamard, symbolisée par H, est une porte quantique unique qui applique une transformation à un qubit. Elle convertit l’état d’un qubit en une superposition uniforme, ce qui est crucial pour créer des états à partir de qubits initialement dans un état déterminé. Cette opération est décrite mathématiquement par la formule suivante :
H = (1/√2) * [[1, 1], [1, -1]]
En appliquant cette matrice à un qubit dans l’état 0, on obtient un état équivalent à une superposition d’états égaux de 0 et 1.
Principes du Test de Hadamard
Le Test de Hadamard consiste à appliquer la matrice H à un qubit, suivi d’une mesure de celui-ci pour observer son état. En fonction de l’importance de la transformation de Hadamard, le test évalue comment un qubit interagit dans un circuit quantique. Il joue un rôle crucial dans la création d’états d’enchevêtrement, où deux ou plusieurs qubits deviennent corrélés de manière à dépendre l’un de l’autre, même lorsque séparés spatialement.
Applications Pratiques du Test de Hadamard
Le Test de Hadamard trouve des applications dans de nombreux algorithmes quantiques, notamment dans des protocoles de cryptographie quantique et dans des algorithmes comme Quantum Fourier Transform. Il permet également de simplifier les circuits quantiques en préparant des états qui peuvent être facilement manipulés par d’autres portes quantiques dans le système. Son utilisation améliore la robustesse et l’efficacité des algorithmes, rendant ainsi la calculabilité quantique plus exploitable.
Conclusion et Perspectives
Le Test de Hadamard est un outil fondamental en informatique quantique qui illustre la puissance des qubits et leur capacité à exister simultanément dans plusieurs états. En comprenant ses principes et ses applications, on peut mieux appréhender les futurs développements et innovations dans ce domaine en pleine expansion. Pour en savoir plus sur la porte de Hadamard, consultez cette ressource.
Le Test de Hadamard représente une innovation majeure en informatique quantique, permettant aux chercheurs d’explorer les fondements même des algorithmes quantiques. En utilisant la transformation de Hadamard, cet outil met en lumière les principes de superposition et d’enchevêtrement, essentiel pour la manipulation des qubits. Ce texte vise à décrire en profondeur le fonctionnement et les applications pratiques du Test de Hadamard, ainsi que son importance dans le développement des technologies quantiques.
Comprendre la transformation de Hadamard
La transformation de Hadamard est une opération clé qui permet de créer des états de superposition dans un système quantique. En agissant sur un qubit, cette transformation permet de transformer un état de base, |0⟩ ou |1⟩, en une combinaison des deux. Cela signifie que, grâce à Hadamard, un qubit peut être simultanément dans les états 0 et 1, une propriété fondamentale qui sous-tend l’informatique quantique.
Les principes du Test de Hadamard
Le Test de Hadamard s’appuie sur l’application de la transformation de Hadamard pour examiner les comportements des qubits. En pratique, cela implique l’utilisation de portes quantiques qui modifient l’état des qubits avant qu’ils ne soient mesurés. En appliquant judicieusement cette transformation, il est possible de déterminer les corrélations entre les états quantiques et d’analyser leur impact sur les calculs.
Applications pratiques du Test de Hadamard
Le Test de Hadamard est utilisé dans de nombreux domaines de recherche, notamment dans la création d’algorithmes quantiques efficaces. Par exemple, il est particulièrement pertinent pour les algorithmes de recherche et d’optimisation qui bénéficient de la capacité de créer des superpositions d’états. Sa flexibilité en fait un outil indispensable pour accélére l’exploration des solutions optimales dans des espaces de recherche complexes.
Conclusion sur l’importance du Test de Hadamard
En somme, le Test de Hadamard joue un rôle crucial dans le développement de l’informatique quantique en offrant une méthode pour explorer les propriétés des qubits. Son intégration dans les algorithmes quantiques ouvre de nouvelles avenues pour des applications qui transcendent les limites des ordinateurs classiques. Pour en savoir plus sur l’importance de cet outil, n’hésitez pas à consulter des ressources supplémentaires disponibles en ligne, telles que cet article sur les portes quantiques.
Le Test de Hadamard, pilier incontournable de l’informatique quantique, représente un outil fondamental permettant d’explorer les caractéristiques uniques des qubits. En transformant les états de base des qubits, ce test ouvre la voie à des calculs en superposition, facilitant ainsi des algorithmes complexes et révolutionnant nos approches traditionnelles du traitement de l’information. Cette opération joue un rôle crucial dans le développement de circuits quantiques, mettant en lumière les principes fondamentaux qui sous-tendent les technologies quantiques modernes.
Le Test de Hadamard est une technique centrale en informatique quantique qui permet d’effectuer des opérations sur des qubits en exploitant les principes de la superposition. Cette méthode, développée à partir de la matrice de Hadamard, facilite la mise en œuvre d’algorithmes quantiques efficaces et permet d’explorer des états quantiques de manière approfondie. Dans cet article, nous allons examiner en détail ce qu’est le Test de Hadamard, son importance, et comment il peut être utilisé comme outil fondamental dans divers domaines de l’informatique quantique.
Définition et Fonctionnement du Test de Hadamard
Le Test de Hadamard est une opération quantique qui transforme les états de base d’un qubit en superposition. En appliquant la matrice de Hadamard, un qubit initialement dans l’état |0⟩ se transforme en une combinaison de |0⟩ et |1⟩, ce qui permet d’explorer un espace d’états beaucoup plus vaste. Cette opération est essentielle pour créer des superpositions nécessaires à la réalisation d’algorithmes quantiques comme ceux de Grover ou de Shor.
Applications Pratiques du Test de Hadamard
Le Test de Hadamard trouve des applications variées, notamment dans les systèmes de cryptographie quantique et dans l’optimisation des algorithmes de recherche. Par exemple, dans le cadre de la cryptographie quantique, cette opération permet de sécuriser les communications en rendant difficile le déchiffrement par des attaquants. De plus, l’utilisation de Hadamard peut optimiser le processus de recherche en permettant de traiter plusieurs solutions simultanément grâce à la superposition.
Conclusion de l’Exploration: Bénéfices et Limites
En tant qu’outil fondamental en informatique quantique, le Test de Hadamard présente de nombreux avantages mais aussi des limites. D’une part, il offre un accès à des états complexes et favorise une meilleure exploitation des ressources quantiques, mais il nécessite également une compréhension approfondie des principes quantiques pour être utilisé efficacement. La maîtrise de cette opération est donc cruciale pour les chercheurs et les praticiens souhaitant avancer dans le domaine de l’informatique quantique.
Le test de Hadamard est une opération clé dans le domaine de l’informatique quantique, jouant un rôle crucial dans la manipulation des qubits. En effet, cette transformation permet de générer des états de superposition, essentiels pour tirer parti des propriétés quantiques, telles que l’enchevêtrement et l’interférence. Comprendre le test de Hadamard est indispensable pour appréhender le comportement et les capacités des algorithmes quantiques.
Mathématiquement, la transformation de Hadamard est représentée par une matrice 2×2, souvent notée H. Cette matrice est définie comme suit :
H = 1/√2 * [1 1]
[1 -1]
Quand cette matrice est appliquée à une entrée de qubit, elle convertit les états de base |0⟩ et |1⟩ en états de superposition. Par exemple, si l’on prend l’état |0⟩ et que l’on applique la matrice de Hadamard, on obtient l’état :
|ψ⟩ = H|0⟩ = (|0⟩ + |1⟩) / √2
Cette transformation conduit à la création d’un état quantique où le qubit a une probabilité égale d’être mesuré dans l’état |0⟩ ou l’état |1⟩. Cette capacité à se trouver dans plusieurs états simultanément est au cœur de l’efficacité des algorithmes quantiques, car elle permet d’explorer simultanément plusieurs solutions à un problème donné.
Le test de Hadamard est particulièrement précieux dans le cadre de l’algorithme de Grover et de l’algorithme de Shor. Par exemple, dans l’algorithme de Grover, utilisé pour la recherche dans une base de données non triée, les portes de Hadamard préparent les qubits pour optimiser les phases suivantes de l’algorithme. Grâce à cette préparation, l’algorithme peut exploiter la superposition pour réduire le nombre de comparaisons nécessaires, offrant ainsi une amélioration significative par rapport aux méthodes classiques.
Dans un autre contexte, lors de l’utilisation de la porte de Hadamard dans la création d’états enchevêtrés, on peut effectuer des calculs quantiques distribués plus efficacement. Cette méthode a des implications importantes pour le développement de la cryptographie quantique et des communications sécurisées, où l’enchevêtrement est utilisé pour garantir la confidentialité et la sécurité des échanges d’informations.
De plus, le test de Hadamard facilite l’implémentation de portes quantiques plus complexes. En agissant comme un « pont » entre les états de base et les états de superposition, les portes de Hadamard permettent de construire des circuits quantiques plus élaborés, pouvant réaliser des tâches computationnelles avancées avec une efficacité accrue.
En résumé, le test de Hadamard est bien plus qu’une simple transformation mathématique. Il représente un élément fondamental dans l’arsenal de l’informatique quantique, permettant de réaliser des opérations complexes, d’optimiser les algorithmes et d’exploiter les phénomènes quantiques. Ce test illustre parfaitement comment les propriétés uniques de la mécanique quantique peuvent offrir des avantages significatifs dans le traitement de l’information, ouvrant la voie à de nouvelles avancées dans le domaine de la technologie quantique.
Le Test de Hadamard est un dispositif essentiel en informatique quantique, permettant d’expliquer et d’analyser les effets des portes quantiques sur les états de qubits. Cet article se propose d’explorer les avantages et les inconvénients liés à l’utilisation de cet outil fondamental dans le cadre des algorithmes quantiques, tout en mettant en lumière les implications de son utilisation dans le traitement et l’analyse des données quantiques.
Avantages
L’un des principaux avantages du Test de Hadamard réside dans sa capacité à produire des superpositions d’états quantiques. En appliquant la transformée de Hadamard à un qubit, il est possible de créer une combinaison d’états, augmentant significativement le potentiel de calcul. Cela permet d’exploiter au mieux la puissance des ordinateurs quantiques, offrant ainsi des vitesses de traitement nettement supérieures à celles des ordinateurs classiques.
De plus, la simplicité du Test de Hadamard en fait un outil d’apprentissage idéal pour introduire les concepts fondamentaux de l’informatique quantique. Les étudiants et les chercheurs peuvent facilement visualiser la transformation des états quantiques, facilitant la compréhension des principes sous-jacents. Les applications de ce test s’étendent également à d’autres algorithmes quantiques, augmentant ainsi son utilité dans divers domaines d’étude.
Inconvénients
Malgré ses nombreux avantages, le Test de Hadamard présente également des inconvénients notables. L’un des plus préoccupants est la sensibilité des états quantiques aux perturbations extérieures. Les qubits, lorsqu’ils sont soumis à des conditions ambiantes telles que le bruit ou les fluctuations thermiques, peuvent perdre leur cohérence, rendant les résultats des algorithmes moins fiables.
En outre, le fonctionnement du Test de Hadamard repose sur des principes théoriques qui peuvent parfois être difficiles à appliquer dans des situations pratiques. Les défis d’implémentation en matière de logiciel et de matériel quantique peuvent limiter l’accès à ces outils pour certains chercheurs. Par conséquent, bien que le Test de Hadamard soit un outil précieux, il nécessite une compréhension approfondie des enjeux associés à l’informatique quantique pour en tirer pleinement parti.
Le Test de Hadamard est une technique incontournable en informatique quantique, permettant de manipuler des qubits avec efficacité. Cet outil utilise la porte d’Hadamard pour créer des superpositions, offrant ainsi une base essentielle pour de nombreux algorithmes quantiques. Dans cet article, nous explorerons le fonctionnement du Test de Hadamard, son importance en informatique quantique et les applications qui en découlent.
Compréhension de la porte d’Hadamard
La porte d’Hadamard est une opération essentielle qui crée une superposition à partir d’un état de base de qubit. Appliquée à un qubit initialement dans l’état |0⟩ ou |1⟩, elle transforme cet état en un mélange des deux, ce qui est fondamental pour le calcul quantique. Par exemple, lorsqu’un qubit dans l’état |0⟩ subit l’opération d’Hadamard, il se retrouve dans un état de superposition positif.
Fonctionnement du Test de Hadamard
Le Test de Hadamard se déroule en plusieurs étapes. Tout d’abord, on applique la porte d’Hadamard à un qubit, créant une superposition. Ensuite, une mesure est effectuée, permettant d’obtenir un résultat qui résonnera avec la probabilité associée à chaque état. Cela établit un lien entre les résultats de la mesure et l’interaction des qubits, servant de fondement pour explorer des comportements quantiques plus complexes.
Applications du Test de Hadamard
Les applications du Test de Hadamard en informatique quantique sont variées. Elle est utilisée dans des algorithmes tels que l’algorithme de Deutsch-Josza et d’autres techniques de recherche quantique. Elle joue également un rôle clé dans la création d’états de Bell, ce qui est essentiel pour les protocoles d’enchevêtrement quantique et pour des applications telles que le téléportation quantique.
En résumé, le Test de Hadamard est un outil fondamental en informatique quantique qui permet de créer et de manipuler des superpositions. Son rôle dans le développement d’algorithmes quantiques et son importance dans l’étude de l’enchevêtrement en font une composante clé de la recherche actuelle en informatique quantique.

Le Test de Hadamard est un concept clé en informatique quantique, permettant d’explorer les propriétés des qubits à travers des opérations fondamentales. Cette technique, qui utilise la transformée de Hadamard, joue un rôle essentiel dans de nombreux algorithmes quantiques, rendant sa compréhension cruciale pour quiconque s’intéresse à ce domaine innovant. Cet article met en lumière les principes de base du Test de Hadamard et son utilisation dans le cadre des circuits quantiques.
Comprendre la Transformée de Hadamard
La transformée de Hadamard est une opération linéaire appliquée sur un qubit qui permet de le placer dans un état de superposition. En effet, elle transforme le qubit de son état de base en une combinaison de ces états, ce qui est fondamental pour réaliser des calculs quantiques. Cette opération est décrite par la matrice H, qui permet de calculer la probabilité de chaque état lors d’une mesure ultérieure.
Applications Pratiques dans les Algorithmes Quantiques
Le Test de Hadamard est souvent utilisé dans des algorithmes comme Grover ou Shor. Grâce à la superposition générée par la transformée de Hadamard, ces algorithmes peuvent évaluer simultanément plusieurs solutions potentielles, offrant ainsi une puissance de calcul exponentielle par rapport aux ordinateurs classiques. La capacité de générer des états combinés est ce qui permet d’accélérer les processus de recherche et de factorisation.
Optimisation des Circuits Quantiques
Dans le cadre des circuits quantiques, le Test de Hadamard est utilisé pour optimiser le chemin d’exécution des algorithmes. En insérant des portes de Hadamard au bon moment, il est possible de réduire le nombre total de portes nécessaires, ce qui minimise les erreurs et augmente l’efficacité globale des circuits. L’analyse de l’impact de la transformée de Hadamard sur la structure des circuits est donc essentielle pour concevoir des systèmes quantiques performants.
État d’Intrication et Superposition
La compréhension du Test de Hadamard est également liée à l’exploration de l’intrication quantique. En combinant des qubits par des portes Hadamard, il est possible de créer des états intriqués, qui sont fondamentaux pour le traitement de l’information quantique. La capacité à manipuler ces états ouvre des perspectives sur des applications telles que le cryptage quantique et les communications ultra-sécurisées.
Défis et Perspectives d’Avenir
Bien que la transformée de Hadamard soit un outil puissant, son utilisation dans les systèmes quantiques pose encore des défis. La maîtrise des techniques d’application et l’optimisation des circuits nécessitent une recherche continue et une innovation technologique. Les avancées dans ce domaine pourraient mener à des découvertes significatives, notamment dans l’amélioration des algorithmes et le développement de nouveaux paradigmes d’informatique quantique.
| Aspect | Détails |
| Définition | Opération fondamentale qui permet de créer des superpositions dans les qubits. |
| Matériel | Utilise une matrice, appelée matrice de Hadamard, pour transformer l’état des qubits. |
| Principe | Transforme les états de base en états superposés, augmentant ainsi le potentiel de calcul. |
| Application | Participe à la création d’algorithmes quantiques tels que l’algorithme de Grover. |
| Importance | Essentiel pour l’exploration et l’utilisation efficace de l’informatique quantique. |
| Impact sur le calcul | Affecte la vitesse et l’efficacité des procédures de recherche dans un espace quantique. |
| Mesure | Facilite la mesure de la probabilité des états après une opération quantique. |
| Complexité | Réduit la complexité des problèmes en transformant les solutions en parallélisme. |

Témoignages sur Le Test de Hadamard : Exploration d’un Outil Fondamental en Informatique Quantique
La découverte du test de Hadamard a marqué un tournant dans ma compréhension de l’informatique quantique. En tant qu’étudiant passionné, j’ai été fasciné par la manière dont cette opération fondamentale transforme les états de base d’un qubit. Grâce à elle, j’ai pu établir des connexions entre les concepts théoriques et leur application pratique, rendant les sessions d’apprentissage bien plus engageantes.
En tant que professionnel dans le domaine, je peux affirmer que le test de Hadamard est une clé pour débloquer des algorithmes quantiques complexes. Son utilisation dans les circuits quantiques m’a permis d’explorer des méthodes de calcul en superposition, offrant des résultats que l’informatique classique aurait peiné à atteindre. C’est un véritable atout pour quiconque souhaite approfondir ses compétences en informatique quantique.
Lors de mes travaux pratiques, j’ai été enchanté par la simplicité du test de Hadamard. L’intégration de cette porte quantique m’a aidé à visualiser les enchevêtrements et à comprendre le comportement unique des qubits. L’aspect interactif des simulations a également enrichi mon expérience d’apprentissage, me permettant d’observer en temps réel comment les états quantiques évoluent.
En suivant des cours en ligne, j’ai pu échanger avec d’autres passionnés et experts sur l’importance du test de Hadamard dans divers algorithmes. Cet échange m’a ouvert les yeux sur des applications pratiques qui vont au-delà de la théorie, notamment dans le domaine du calcul quantique et du traitement de l’information. L’enthousiasme partagé autour de ce sujet a renforcé mon désir de m’investir davantage dans l’informatique quantique.
Enfin, j’encourage tous ceux qui s’intéressent à l’informatique quantique de ne pas négliger le test de Hadamard. C’est un outil fondamental qui, selon moi, est essentiel pour construire une base solide dans ce domaine dynamique. J’attends avec impatience de voir comment des innovations futures s’appuieront sur cette opération pour transformer encore davantage notre compréhension et utilisation des technologies quantiques.
Introduction au Test de Hadamard
Le Test de Hadamard est un outil essentiel dans le domaine de l’informatique quantique, offrant des applications variées allant de la cryptographie quantique à la simulation de systèmes quantiques. Cette méthode utilise la matrice de Hadamard pour transformer des états quantiques, permettant ainsi de réaliser des calculs complexes tout en préservant les propriétés fondamentales des qubits. Cet article plonge profondément dans les principes et les applications du Test de Hadamard, en soulignant son rôle crucial dans le développement de technologies quantiques avancées.
Définition et Fonctionnement de la Matrice de Hadamard
La matrice de Hadamard, notée H, est définie comme suit :
H = 1/√2 * |0⟩ + |1⟩
1/√2 * |0⟩ – |1⟩
Cette matrice joue un rôle crucial dans le processus de transformation d’un qubit. En appliquant la matrice de Hadamard à un qubit en état de base |0⟩ ou |1⟩, on obtient une superposition d’états. Cela signifie que le qubit peut exister simultanément dans plusieurs états, ce qui est fondamental pour l’informatique quantique. Le Test de Hadamard exploite cette propriété de superposition, ouvrant la voie à des calculs nouveaux et innovants.
Importance dans les Algorithmes Quantiques
Le Test de Hadamard est au cœur de nombreux algorithmes quantiques, dont le célèbre algorithme de Grover et l’algorithme de Shor. Grâce à sa capacité à générer de la superposition, il permet d’explorer des solutions multiples à un problème de manière simultanée. Cette approche radicale réduit le temps de calcul par rapport aux algorithmes classiques, qui doivent traiter chaque solution de manière séquentielle. Ainsi, les applications pratiques du Test de Hadamard s’étendent à des domaines comme l’optimisation, la recherche dans les bases de données, et même la cryptographie.
Application du Test de Hadamard dans la Simulations
Dans le contexte des simulations quantiques, le Test de Hadamard est utilisé pour reproduire le comportement de systèmes quantiques complexes. Par exemple, dans la simulation de l’interaction entre particules, le Test de Hadamard peut être appliqué pour évaluer les états d’énergie et les transitions entre états quantiques. Grâce à cette technique, les chercheurs peuvent mieux comprendre des phénomènes physiques qui étaient auparavant inaccessibles avec des méthodes classiques, ouvrant des possibilités nouvelles dans des domaines comme la physique des particules et la chimie quantique.
Challenges Associés au Test de Hadamard
Malgré ses nombreux avantages, l’application du Test de Hadamard présente également des défis techniques. L’un des principaux obstacles est la décorrélation des états quantiques, qui peut survenir lorsque plusieurs opérations de Hadamard sont appliquées successivement. Cela peut entraîner une perte d’informations précieuses, réduisant ainsi l’efficacité des calculs. De plus, la mise en œuvre pratique du Test de Hadamard nécessite une maîtrise précise des dispositifs quantiques disponibles sur le marché, ce qui peut s’avérer complexe pour les chercheurs et les développeurs.
En somme, le Test de Hadamard se révèle être un élément fondamental en informatique quantique. Sa capacité à créer des superpositions d’états quantiques et à contribuer efficacement aux algorithmes quantiques le place au cœur des innovations technologiques modernes. Bien que des défis subsistent, l’exploration continue de cet outil promet d’ouvrir de nouvelles portes dans l’univers fascinant de la technologie quantique.
Comparaison des Approches du Test de Hadamard en Informatique Quantique
| Aspect | Description |
| Définition | Opération quantique transformant les états de base d’un qubit en superposition. |
| Matricielle | Représentée par la matrice de Hadamard : H = (1/√2) * [[1, 1], [1, -1]]. |
| Impact sur les qubits | Génère une équité entre les états |0⟩ et |1⟩, optimisant la phase quantique. |
| Applications | Essentielle dans les algorithmes quantiques comme Grover et Shor. |
| Complexité | Utilisation d’un simple qubit pour un impact considérable sur l’informatique quantique. |
| Simulations | Facilite la modélisation de circuits quantiques et l’expérimentation en temps réel. |
| Enchevêtrement | Permet de créer des états intriqués, augmentant la puissance de calcul. |

Le Test de Hadamard émerge comme un élément central dans le domaine de l’informatique quantique, jouant un rôle crucial dans la manipulation des qubits. Cet outil fondamental permet de transformer des états quantiques et d’exploiter les principes de superposition et d’enchevêtrement, jetant les bases des algorithmes quantiques avancés. Dans cette étude de cas, nous examinerons en profondeur le fonctionnement et les applications du Test de Hadamard, ainsi que son importance dans le développement de l’informatique quantique moderne.
Qu’est-ce que le Test de Hadamard ?
Le Test de Hadamard est une opération quantique appliquée pour transformer un qubit en un état de superposition. Représenté par la matrice de Hadamard, ce test agit sur un état de base, le rendant capable d’exister simultanément dans plusieurs états. En effectuant le Test de Hadamard sur un qubit initialement en état |0⟩, le résultat est une superposition de |0⟩ et |1⟩ avec des amplitudes égales. Cette capacité à générer des superpositions est essentielle pour réaliser des calculs quantiques complexes.
Fonctionnement du Test de Hadamard
Le Test de Hadamard se base sur une matrice de transformation spécifique, souvent notée H. Lorsque H est appliquée à un qubit, chaque élément de l’état quantique est affecté individuellement, permettant ainsi une combinaison précise des probabilités. En termes mathématiques, la transformation de Hadamard peut s’écrire comme suit : H|0⟩ = (|0⟩ + |1⟩)/√2 et H|1⟩ = (|0⟩ – |1⟩)/√2. Cela signifie que le qubit est désormais dans une superposition d’états, indispensable pour les algorithmes quantiques.
Applications du Test de Hadamard
Le Test de Hadamard trouve une multitude d’applications dans le développement d’algorithmes quantiques. Par exemple, il est utilisé dans l’algorithme de Grover pour la recherche non structurée, ainsi que dans l’algorithme de Shor pour la factorisation des entiers. Dans ces contextes, le Test de Hadamard optimise considérablement la rapidité des calculs par rapport à leurs équivalents classiques. De plus, son utilisation dans les circuits quantiques permet de créer des états d’enchevêtrement, élément clé des systèmes quantiques.
Importance dans le domaine de l’informatique quantique
Le Test de Hadamard joue un rôle crucial dans la compréhension des propriétés fondamentales des systèmes quantiques. Son impact sur l’enchevêtrement et la superposition est essentiel pour avancer dans le développement d’ordinateurs quantiques plus puissants. L’intégration de ce test dans des circuites quantiques contribue aussi à une meilleure efficacité dans l’exécution des algorithmes, ouvrant la voie à des applications innovantes dans divers domaines, tels que la cryptographie quantique et l’optimisation.
Le test de Hadamard représente une avancée considérable dans le domaine de l’informatique quantique. En tant qu’opération essentielle, elle permet de créer des superpositions d’états quantiques, ce qui est fondamental pour l’exploitation des propriétés uniques des qubits. Cette manipulation ouvre la voie à des algorithmes plus efficaces que ceux basés sur des approches classiques, facilitant des calculs complexes qui seraient autrement inaccessibles.
L’utilisation de la transformation de Hadamard joue un rôle crucial dans l’élaboration d’algorithmes quantiques. Grâce à sa capacité à prendre un état de qubit pur et à le transformer en une superposition, elle permet non seulement de maximiser la puissance de calcul, mais aussi d’explorer des chemins multiples simultanément. Cela confère aux ordinateurs quantiques un avantage stratégique par rapport aux ordinateurs classiques, notamment dans des domaines tels que la cryptographie, la simulation de systèmes complexes, et l’optimisation de problèmes.
Cependant, pour tirer pleinement parti du test de Hadamard, il est essentiel de comprendre son application dans le cadre des circuits quantiques. Les portes quantiques, dont fait partie la porte de Hadamard, s’intègrent dans un cadre plus large qui nécessite des connaissances solides en physique quantique et en théorie de l’information. Des études approfondies permettront de mieux appréhender l’impact de cette transformation sur la manière dont les qubits interagissent et comment les résultats peuvent être mesurés.
Il s’avère donc que le test de Hadamard ne se limite pas à une simple opération : c’est un pilier sur lequel repose une grande partie des avancées en matière de calcul quantique. En continuant d’explorer et d’expérimenter avec cet outil, la communauté scientifique pave la voie à des découvertes novatrices qui pourraient révolutionner de nombreux secteurs d’activité.
FAQ sur le Test de Hadamard
Q : Qu’est-ce que le Test de Hadamard en informatique quantique ?
R : Le Test de Hadamard est un outil utilisé pour créer des superpositions d’états quantiques, permettant ainsi d’exploiter le pouvoir des qubits en informatique quantique.
Q : Pourquoi le Test de Hadamard est-il si important ?
R : Il est crucial car il permet de réaliser des opérations de calcul quantique efficaces, en facilitant la création de l’enchevêtrement et des interférences quantiques nécessaires aux algorithmes quantiques.
Q : Comment fonctionne le Test de Hadamard ?
R : Le Test de Hadamard applique une transformation à un qubit, permettant de passer d’un état classique à une superposition d’états, ce qui est fondamental pour la manipulation de l’information quantique.
Q : Quel est l’impact du Test de Hadamard sur les algorithmes quantiques ?
R : Il améliore l’efficacité des algorithmes quantiques en augmentant le nombre d’états pouvant être explorés simultanément, ce qui réduit le temps de calcul pour certaines tâches complexes.
Q : Peut-on visualiser le fonctionnement du Test de Hadamard ?
R : Oui, il est possible de le visualiser à l’aide de diagrammes représentant les portes quantiques et les transformations appliquées aux qubits, facilitant ainsi la compréhension du processus.
Q : Le Test de Hadamard est-il utilisé dans des applications pratiques ?
R : Absolument, il est utilisé dans divers algorithmes quantiques, notamment ceux liés à la recherche, à la cryptographie et à l’optimisation, montrant son utilité en informatique quantique moderne.
Le Test de Hadamard est une opération cruciale dans le domaine de l’informatique quantique, jouant un rôle indispensable dans divers algorithmes quantiques, notamment ceux qui exploitent la superposition. Cette opération utilise la matrice de Hadamard pour transformer les états quantiques d’un qubit et créer une superposition d’états, permettant d’effectuer des calculs parallèles. Le Test de Hadamard est souvent considéré comme une porte quantique fondamentale et sert d’introduction aux conceptions plus complexes d’algorithmes quantiques.
La matrice de Hadamard, notée H, est une matrice 2×2 qui s’exprime par les valeurs suivantes : H = (1/√2) * [1 1; 1 -1]. Lorsqu’un qubit est soumis à cette transformation, il passe d’un état déterminé à un état en superposition, ce qui signifie qu’il peut exister simultanément dans plusieurs états quantiques. Ce phénomène est à la base de la puissance des ordinateurs quantiques, car il permet d’explorer un vaste espace de solutions en un temps réduit.
Pour illustrer le fonctionnement du Test de Hadamard, prenons un qubit initialement dans l’état |0⟩. Lorsque la matrice de Hadamard est appliquée, le qubit se transforme en l’état (|0⟩ + |1⟩) / √2. Ce nouvel état est une superposition, ce qui signifie que le qubit a maintenant une probabilité de 50 % d’être mesuré en tant que |0⟩ ou |1⟩. Cette capacité à générer des superpositions est primordiale pour des algorithmes comme Deutsch-Josza ou encore l’algorithme de Grover, qui reposent sur l’exploitation de plusieurs chemins computationnels simultanément.
Le Test de Hadamard joue également un rôle fondamental dans le phénomène d’enchevêtrement. Lorsqu’il est appliqué à un système de plusieurs qubits, il génère des corrélations intriquées entre les qubits, permettant ainsi d’effectuer des calculs d’une complexité accrue. L’enchevêtrement est un principe clé qui permet aux ordinateurs quantiques de surpasser leurs homologues classiques dans certains types de problèmes.
Un autre aspect primordial du Test de Hadamard est son interaction avec l’appariement des qubits. Dans plusieurs algorithmes, on réalise d’abord un Test de Hadamard sur un ensemble de qubits, avant de les manipuler davantage. Cela permet d’établir des états cohérents qui peuvent ensuite être mesurés pour extraire des informations précieuses sur des systèmes complexes.
En raison de son importance, le Test de Hadamard est souvent l’un des premiers concepts enseignés aux étudiants en informatique quantique. Comprendre cette opération ouvre la voie à la maîtrise des algorithmes plus avancés et fournit une base solide pour explorer les capacités uniques des ordinateurs quantiques.
Dans la pratique, la mise en œuvre du Test de Hadamard peut se faire à travers différentes plateformes de programmation quantique, qui permettent de simuler et d’appliquer ces opérations sur des qubits en utilisant des environnements codifiés. Cela inclut des langages tels que Qiskit ou Cirq, qui offrent des outils pour les chercheurs et les praticiens souhaitant explorer le monde fascinant de l’informatique quantique.
En conclusion, le Test de Hadamard est non seulement un outil fondamental en informatique quantique, mais aussi un concept qui illustre les possibilités infinies que cette discipline émergente a à offrir. Grâce à sa capacité à générer des superpositions et des enchevêtrements, le Test de Hadamard est un élément clé pour comprendre le comportement unique des qubits et la puissance des systèmes quantiques dans leur ensemble.
Mon expérience avec Quantum AI a été véritablement transformative. En tant qu’expert en informatique quantique, j’ai été particulièrement impressionné par la facilité d’utilisation de cette plateforme. Dès mon inscription, l’interface s’est révélée intuitive, permettant une navigation rapide et fluide. Les différentes sections étaient bien organisées, ce qui a facilité la recherche des ressources dont j’avais besoin.
Les services offerts sont d’une qualité exceptionnelle. Les webinaires et les cours en ligne dispensés par des experts de renom m’ont permis d’approfondir mes connaissances sur des sujets complexes tels que les algorithmes quantiques et les applications pratiques des qubits. De plus, les simulations interactives m’ont donné l’opportunité de mettre en pratique mes théories de manière sécurisée, sans risquer mon capital.
Grâce à cette plateforme, j’ai observé une nette amélioration de mes résultats financiers. La combinaison de l’analyse de marché en temps réel et des outils de gestion des risques proposés par Quantum AI m’a permis de prendre des décisions éclairées et d’optimiser mes investissements. Chaque décision, informée par des données précises, a renforcé ma confiance et ma compétence en matière de trading.
Je recommande vivement Quantum AI à tous ceux qui s’intéressent à l’investissement et à l’informatique quantique. Que vous soyez débutant ou expérimenté, cette plateforme s’adapte à vos besoins et vous offre un accompagnement inestimable. Rejoindre cette communauté dynamique d’investisseurs passionnés a été une des meilleures décisions de ma carrière. Ne manquez pas l’opportunité de découvrir tout ce que Quantum AI peut vous offrir.